2020年上海高考数学答案解析
1.已知集合A={1,2,4},B={2,3,4},求A∩B=
答案:
{2,4}
1/3
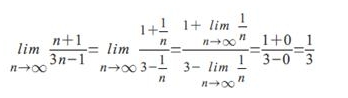
3.已知复数z满足z=1-2i(i为虚数单位),则|z|=_____
答案:
√5
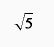
5.已知f(x)=x3,则f-1(x)=________
答案: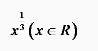
6. 已知a、b、1、2的中位数为3,平均数为4,则ab=
答案:36
8.已知{an}是公差不为零的等差数列,且a1+a10=a9,则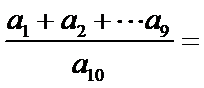 _______
_______
答案:27/8
9.从6人中挑选4人去值班,每人值班1天,第一天需要1人,第二天需要1人,第三天需要2人,则有 种排法。
答案:180
10. 椭圆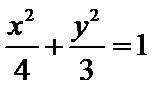 ,过右焦点F作直线
,过右焦点F作直线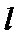 交椭圆于P、Q两点,P在第二象限已知
交椭圆于P、Q两点,P在第二象限已知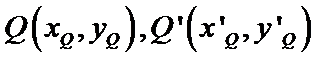 都在椭圆上,且
都在椭圆上,且 ,
,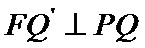 ,则直线
,则直线 的方程为
的方程为
答案:x+y-1=0
11、设a∈R,若存在定义域R的函数f(x)既满足对于任意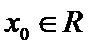 ,
,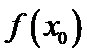 的值为
的值为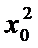 或
或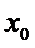 ”又满足“关于
”又满足“关于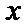 的方程
的方程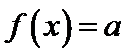 无实数解”,则
无实数解”,则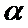 的取值范围为
的取值范围为
答案:
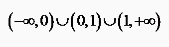
12、已知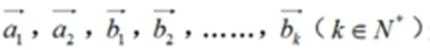 是平面内两两互不平等的向量,满足
是平面内两两互不平等的向量,满足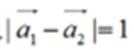 ,且
,且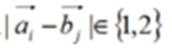 (其中
(其中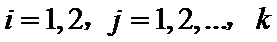 ),则K的最大值为
),则K的最大值为
答案:6
13、下列不等式恒成立的是()
答案:B
14、已知直线l的解析式为3x-4y+1=0,则下列各式是l的参数方程的是__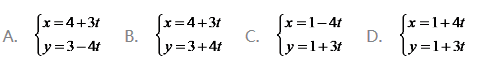
答案:D
16.、若存在a∈R且a≠0,对任意的x∈R,均有f(x+a)<f(x)+f(a)恒成立,则称函数f(x)具有性质P,已知: 单调递减,且
单调递减,且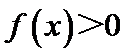 恒成立;
恒成立;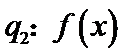 单调递增,存在
单调递增,存在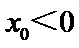 使得
使得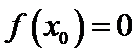 ,则是
,则是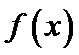 具有性质
具有性质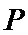 的充分条件是()
的充分条件是()
答案:C
17、已知边长为1的正方形ABCD,沿BC旋转一周得到圆柱体。 (1)求圆柱体的表面积; (2)正方形ABCD绕BC逆时针旋转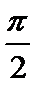 到
到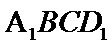 ,求
,求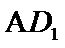 与平面ABCD所成的角。
与平面ABCD所成的角。
答案:(1)4π
(2)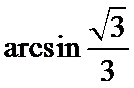
18、已知 (1)若f(x)的周期是4π,求 (2)已知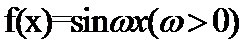 .
.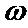 ,并求此时
,并求此时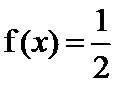 的解集;
的解集; ,
, ,
,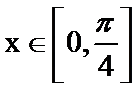 ,求g(x)的值域.
,求g(x)的值域.
答案:
(1)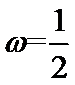 ,
,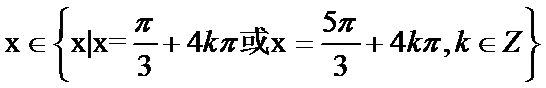 (2)
(2)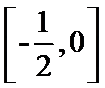
19、已知: (1)若v>95,求x的取值范围; (2)已知x=80时,v=50,求x为多少时,q可以取得最大值,并求出该最大值。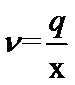 ,
,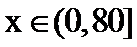 ,且
,且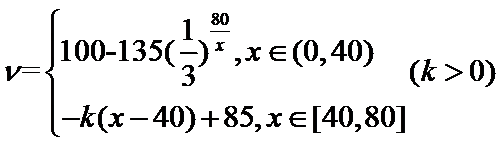 ,
,
答案:
(1)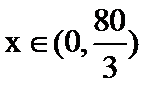 (2)
(2)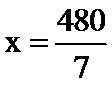 时,
时,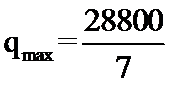
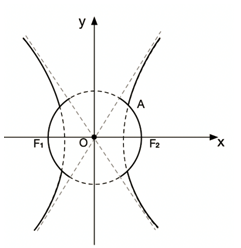
20、双曲线 (1)若 (2)若 (3)过点 ,圆
,圆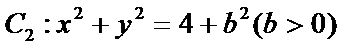 在第一象限交点为A,
在第一象限交点为A,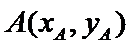 ,曲线
,曲线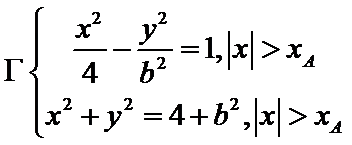 。
。
 ,求b;
,求b; ,
, 与x轴交点记为
与x轴交点记为 ,P
,P 是曲线
是曲线 上一点,且在第一象限,并满足
上一点,且在第一象限,并满足 ,求∠
,求∠ ;
; 且斜率为
且斜率为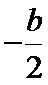 的直线
的直线 交曲线
交曲线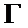 于M、N两点,用b的代数式表示
于M、N两点,用b的代数式表示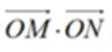 ,并求出
,并求出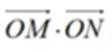 的取值范围。
的取值范围。
答案:(1)2
(2)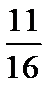 (3)
(3)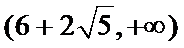 ;
;
21.有限数列{an},若满足 (1)判断数列3,2,5,1和4,3,2,5,1是否具有性质,请说明理由 (2)若a1=1,公比为9的等比数列,项数为10,具有性质P,求q的取值范围. (3) 若 ,m是项数,则称{an}满足性质P.
,m是项数,则称{an}满足性质P.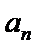 是
是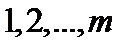 的一个排列
的一个排列 都具有性质
都具有性质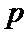 ,求所有满足条件的
,求所有满足条件的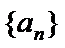 .
.
答案:
(1)对于第一个数列有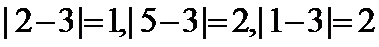 ,
满足题意,该数列满足性质
,
满足题意,该数列满足性质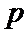 对于第二个数列有
对于第二个数列有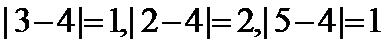 不满足题意,该数列不满足性质
不满足题意,该数列不满足性质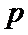 .
.







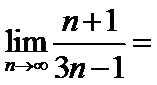 (lim n+1/3n-1)________
(lim n+1/3n-1)________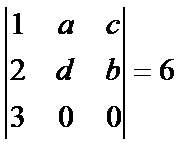 ,则行列式
,则行列式 _______
_______
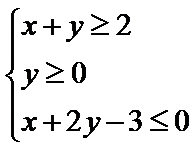 ,则z=y-2x的最大值为______
,则z=y-2x的最大值为______