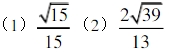2020年江苏高考数学答案解析
1.已知集合A={-1,0,1,2},B={0,2,3},则A∩B=
答案:
{0,2}
2.已知是i虚数单位,则复数z=(1+i)(2-i)的实部是________
答案:
3
3. 已知一组数据4,2a,3-a,5,6的平均数为4,则a的值是__________。
答案:
2
4. 将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是________。
答案:
1/9
5. 右图是一个算法流程图,若输出y的值为-2,则输入x的值为______。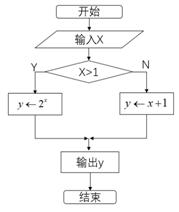
答案:
-3
6.在平面直角坐标系xOy中y=22,若双曲线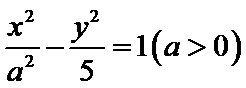 的一条渐近线方程为
的一条渐近线方程为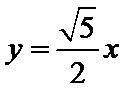 ,则该双曲线的离心率是_________
,则该双曲线的离心率是_________
答案:
3/2
7.已知y=f(x)是奇函数,当x>0时,,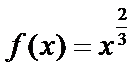 ,则
,则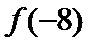 的值是________。
的值是________。
答案:
-4
1/3
9. 如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的,已知螺帽的底面正六边形边长为2cm,高为2cm,内孔半径为0.5cm,则此六角螺帽毛坯的体积是________cm3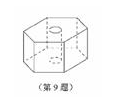
答案:
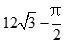
12√3-π/2
10. 将函数 的图像向右平移
的图像向右平移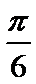 个单位长度,则平移后的图像与
个单位长度,则平移后的图像与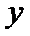 轴最近的对称轴方程是_______ 。
轴最近的对称轴方程是_______ 。
答案:
-5π/24
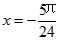
11.设{an}是公差为d的等差数列,{bn}是公比为的等比数列,已知数列{an+bn}的前项和 ,则
,则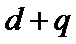 的值是 ______________。
的值是 ______________。
答案:
4
12.已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值是______________
答案:
4/5
13.在△ABC中,AB=4,AC=3,∠BAC=90°,D在边AC上,延长AD到P,使得AP=9,若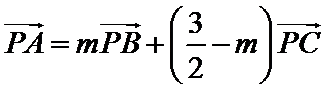 ___(m为常数),则CD的长度是________________
___(m为常数),则CD的长度是________________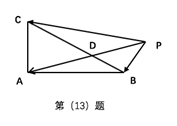
答案:
18/5或0
14.在平面直角坐标系xOy中,已知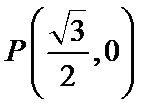 ,A,B是圆
,A,B是圆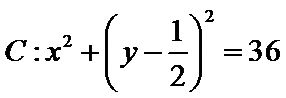 上的两个动点,满足PA=PB,则△PAB的面积的最大值是_______
上的两个动点,满足PA=PB,则△PAB的面积的最大值是_______
答案:
10√5
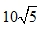
15.在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E、F分别是AC、B1C的中点 (1)求证:EF平面AB1C1; (2)求证:平面AB1C⊥平面ABB1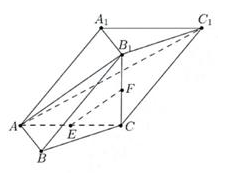
答案:

16.在△ABC中,角A、B、C的对边分别为a、b、c,已知a=3, (1)求 (2)在边BC上取一点D,使得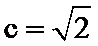 ,B=45°.
,B=45°.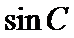 的值;
的值;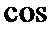 ∠
∠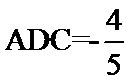 ,求
,求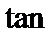 ∠DAC的值。
∠DAC的值。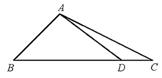
答案:
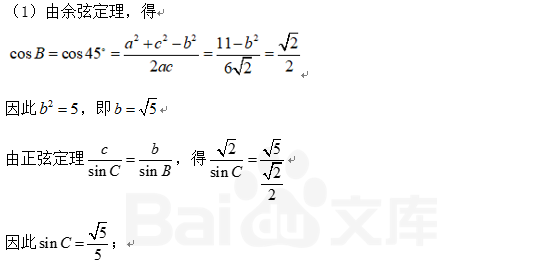

19.已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).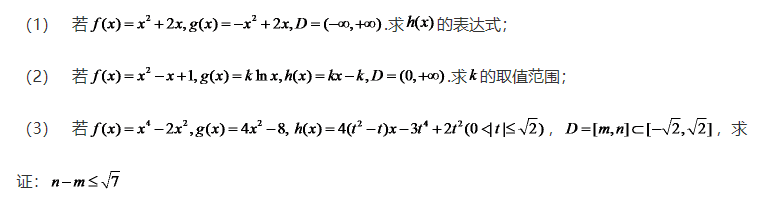
答案:




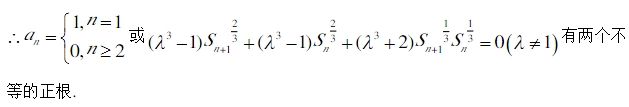
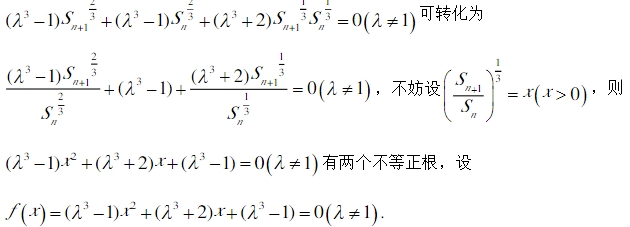


21.平面上点A(2,-1)在矩阵M=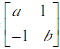 对应的变换作用下得到点B(3,4)
对应的变换作用下得到点B(3,4)
(1)求实数a,b的值;
(2)求矩阵M的逆矩阵M-1
答案: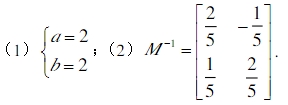
22.在极坐标系中,已知点A(p1,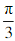 )在直线/:pcosθ=2上,点B(p2,
)在直线/:pcosθ=2上,点B(p2,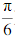 ),在圆C:p=4sinθ上(其中p≥0,0≤θ<2π)
),在圆C:p=4sinθ上(其中p≥0,0≤θ<2π)
(1)求p1,P2的值
(2)求出直线/与圆C的公共点的极坐标
答案:(1)P1=4,P2=2(2)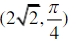



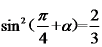 ,则sin2a的值是_______。
,则sin2a的值是_______。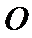 在水平线
在水平线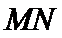 上,桥
上,桥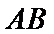 与
与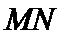 平行,
平行, 为铅垂线(
为铅垂线(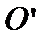 在
在 上),经测量,左侧曲线
上),经测量,左侧曲线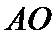 上任--点
上任--点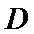 到
到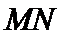 的距离
的距离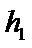 (米)与
(米)与 到
到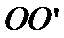 的距离
的距离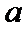 (米)之间满足关系式
(米)之间满足关系式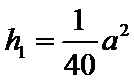 ;右侧曲线
;右侧曲线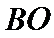 上任一点
上任一点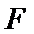 到
到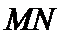 的距离
的距离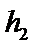 (米)与
(米)与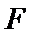 到
到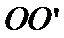 的距离
的距离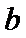 (米)之间满足关系式
(米)之间满足关系式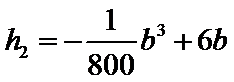 。已知点
。已知点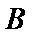 到
到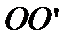 的距离为40米。
的距离为40米。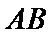 的长度;
的长度;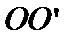 的桥墩
的桥墩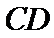 和
和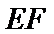 。且
。且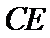 为80米,其中
为80米,其中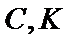 在
在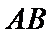 上(不包括端点)。桥墩
上(不包括端点)。桥墩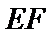 每米造价
每米造价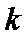 (万元)。桥墩
(万元)。桥墩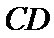 每米造价
每米造价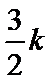 (万元)
(万元) 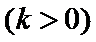 ,问
,问 为多少米时,桥墩
为多少米时,桥墩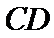 与
与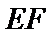 的总造价最低?
的总造价最低?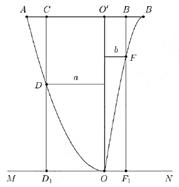

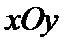 中,若椭圆
中,若椭圆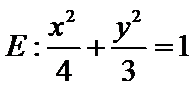 的左、右焦点分别为
的左、右焦点分别为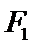 ,
,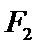 ,点
,点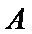 在椭圆
在椭圆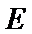 上且在第一象限内,
上且在第一象限内,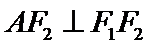 ,直线
,直线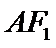 与椭圆
与椭圆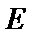 相交于另一点
相交于另一点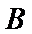 。
。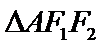 的周长;
的周长; 轴上任取一点
轴上任取一点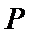 ,直线
,直线 与椭圆
与椭圆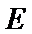 的右准线相交于点
的右准线相交于点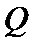 ,求
,求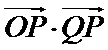 的最小值;
的最小值;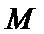 在椭圆
在椭圆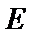 上,记
上,记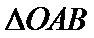 与
与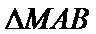 的面积分别是
的面积分别是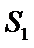 ,
, ,若
,若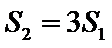 ,求
,求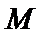 的坐标。
的坐标。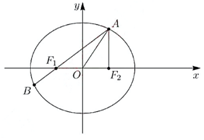



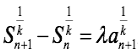 成立,则称此为“λ-k”数列。
成立,则称此为“λ-k”数列。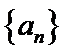 是
是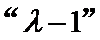 数列,求
数列,求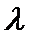 的值:
的值: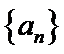 是
是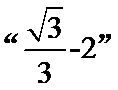 数列,且
数列,且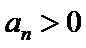 ,求数列
,求数列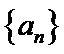 的通项公式:
的通项公式: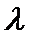 ,是否存在三个不同的数列
,是否存在三个不同的数列 为
为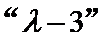 数列,且
数列,且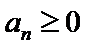 ?若存在,求
?若存在,求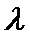 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。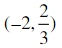
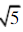 ,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.
,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.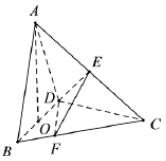
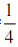 BC,设二面角F--DE--C的大小为θ,求sinθ的值.
BC,设二面角F--DE--C的大小为θ,求sinθ的值.