2019全国二卷文科数学解析
1.已知集合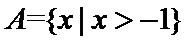 ,
,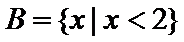 ,则A∩B=
,则A∩B=
答案:C
2.设z=i(2+i),则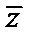 =
=
答案:D
3.已知向量a=(2,3),b=(3,2),则|a-b|=
答案:A
4.生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为
答案:B
6.设f(x)为奇函数,且当x≥0时,f(x)= ,则当x<0时,f(x)=
,则当x<0时,f(x)=
答案:D
8.若x1=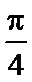 ,x2=
,x2=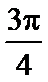 是函数f(x)=
是函数f(x)=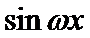 (
(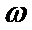 >0)两个相邻的极值点,则
>0)两个相邻的极值点,则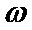 =
=
答案:A
9.若抛物线y2=2px(p>0)的焦点是椭圆 的一个焦点,则p=
的一个焦点,则p=
答案:D
10.曲线y=2sinx+cosx在点(π,-1)处的切线方程为
答案:C
11.已知a∈(0, ),2sin2α=cos2α+1,则sinα=
),2sin2α=cos2α+1,则sinα=
答案:B
12.设F为双曲线C: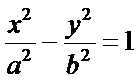 (a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若|PQ|=|OF|,则C的离心率为
(a>0,b>0)的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2交于P、Q两点.若|PQ|=|OF|,则C的离心率为
答案:A
13.若变量x,y满足约束条件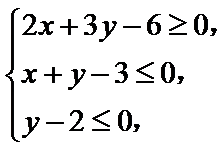 则z=3x–y的最大值是___________.
则z=3x–y的最大值是___________.
答案:
9
0.98
15.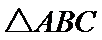 的内角A,B,C的对边分别为a,b,c.已知bsinA+acosB=0,则B=___________.
的内角A,B,C的对边分别为a,b,c.已知bsinA+acosB=0,则B=___________.
答案:
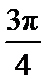
26;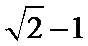
17.(12分) 如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1. (1)证明:BE⊥平面EB1C1; (2)若AE=A1E,AB=3,求四棱锥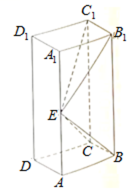

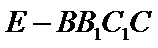 的体积.
的体积.
答案:
四棱锥E-BB1C1C的体积为18,看解析
18.(12分) 已知 (1)求 (2)设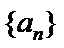 是各项均为正数的等比数列,
是各项均为正数的等比数列,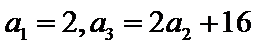 .
.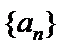 的通项公式;
的通项公式;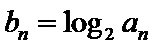 ,求数列
,求数列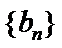 的前n项和.
的前n项和.
答案:
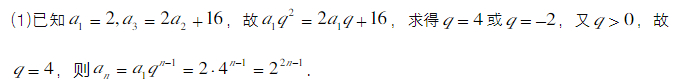 看解析
看解析
 看解析
看解析
20.(12分) 已知 (1)若 (2)如果存在点P,使得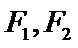 是椭圆
是椭圆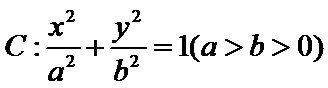 的两个焦点,P为C上一点,O为坐标原点.
的两个焦点,P为C上一点,O为坐标原点.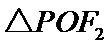 为等边三角形,求C的离心率;
为等边三角形,求C的离心率;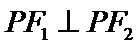 ,且
,且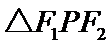 的面积等于16,求b的值和a的取值范围.
的面积等于16,求b的值和a的取值范围.
答案:
(1)连结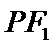 ,由
,由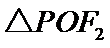 为等边三角形可知在
为等边三角形可知在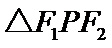 中,更多看解析
中,更多看解析
21.(12分) 已知函数 (1) (2)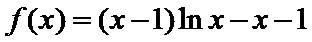 .证明:
.证明: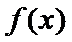 存在唯一的极值点;
存在唯一的极值点; 有且仅有两个实根,且两个实根互为倒数.
有且仅有两个实根,且两个实根互为倒数.
答案:
 更多看解析》》》
更多看解析》》》
 更多查看解析》》》
更多查看解析》》》
23.[选修4-5:不等式选讲](10分) 已知 (1)当 (2)若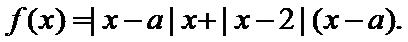
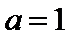 时,求不等式
时,求不等式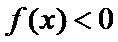 的解集;
的解集;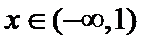 时,
时, ,求
,求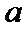 的取值范围.
的取值范围.
答案:
(1)当a=1时,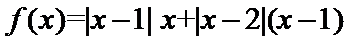 .
.
当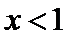 时,
时,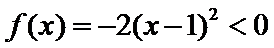 ;当
;当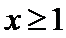 时,
时,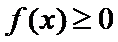 .
.
所以,不等式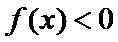 的解集为
的解集为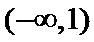 .
.



 (1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;
(1)分别估计这类企业中产值增长率不低于40%的企业比例、产值负增长的企业比例;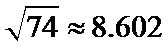 .
.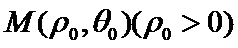 在曲线
在曲线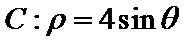 上,直线l过点
上,直线l过点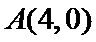 且与
且与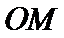 垂直,垂足为P.
垂直,垂足为P.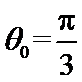 时,求
时,求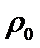 及l的极坐标方程;
及l的极坐标方程;