2019全国一卷文数答案解析
1.设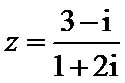 ,则
,则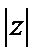 =
=
答案:C
2.已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则
答案:C
3.已知 a=log20.2,b=20.2,c=0.20.3 ,则
答案:B
6.某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是
答案:C
7.tan255°=
答案:D
8.已知非零向量a,b满足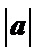 =2
=2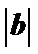 ,且(a-b)
,且(a-b)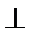 b,则a与b的夹角为
b,则a与b的夹角为
答案:B
10.双曲线C: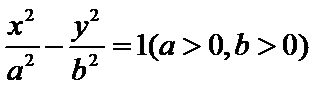 的一条渐近线的倾斜角为130°,则C的离心率为
的一条渐近线的倾斜角为130°,则C的离心率为
答案:D
11.△ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA=-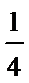 ,则
,则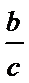 =
=
答案:A
12.已知椭圆C的焦点为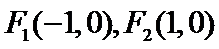 ,过F2的直线与C交于A,B两点.若
,过F2的直线与C交于A,B两点.若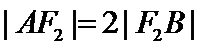 ,
,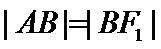 ,则C的方程为
,则C的方程为
答案:B
y=3x
14.记Sn为等比数列{an}的前n项和.若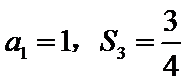 ,则S4=___________.
,则S4=___________.
答案:
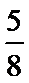
−4
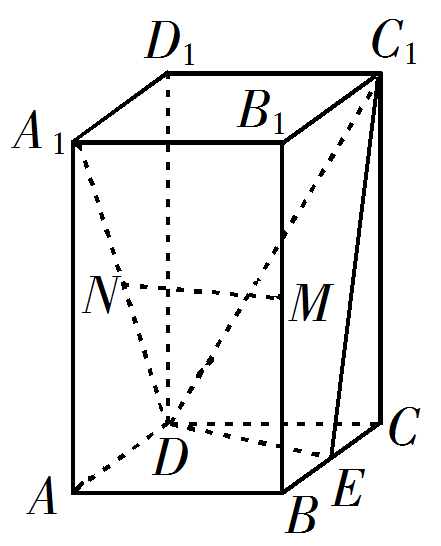
16.已知∠ACB=90°,P为平面ABC外一点,PC=2,点P到∠ACB两边AC,BC的距离均为 ,那么P到平面ABC的距离为___________.
,那么P到平面ABC的距离为___________.
答案:
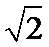
18.(12分) 记Sn为等差数列{an}的前n项和,已知S9=-a5. (1)若a3=4,求{an}的通项公式; (2)若a1>0,求使得Sn≥an的n的取值范围.
23.[选修4−5:不等式选讲](10分) 已知a,b,c为正数,且满足abc=1.证明: (1) (2) ;
;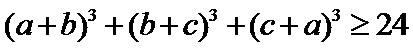 .
.



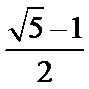 (
(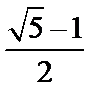 ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是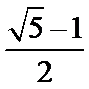 .若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105 cm,头顶至脖子下端的长度为26 cm,则其身高可能是
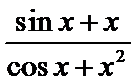 在[-π,π]的图像大致为
在[-π,π]的图像大致为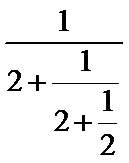 的程序框图,图中空白框中应填入
的程序框图,图中空白框中应填入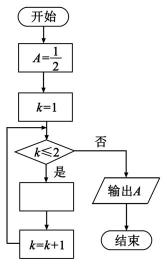
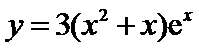 在点
在点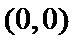 处的切线方程为___________.
处的切线方程为___________.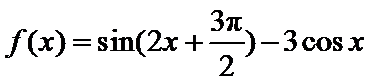 的最小值为___________.
的最小值为___________.

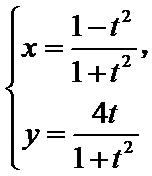 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为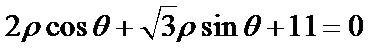 .
.