2018年天津高考理数答案解析
1.设全集为R，集合A={x|0<x<2},B={x|x>=1}则AI(δRB)=
答案:B
2. 设变量x，y满足约束条件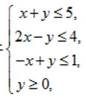
则目标函数z=3x+5y的最大值为
答案:C
3.阅读如图的程序框图，运行相应的程序，若输入N的值为20，则输出T的值为
答案:B
4. 设x∈R，则“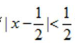
”是“x3<1”的
答案:A
5. 已知a=log2e，b=ln2，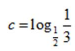
，则a，b，c的大小关系为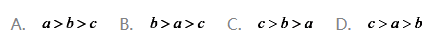 
答案:D
6. 将函数y=sin(2x+π/5)的图象向右平移π/10个单位长度，所得图象对应的函数
答案:A
7. 已知双曲线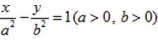
的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点. 设A，B到双曲线同一条渐近线的距离分别为d1和d2，且d1+d2=6，则双曲线的方程为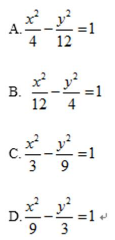
答案:C
8. 如图，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAD=120°，AB=AD=1. 若点E为边CD上的动点，则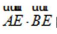
的最小值为 
答案:A
9. i是虚数单位，复数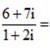
___________.
答案:【答案】4–i
10. 在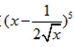
的展开式中，X2的系数为____________.
答案:5/2
11. 已知正方体ABCD-A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥
的体积为 .
答案:1/12
12.已知圆x2+y2-2x=0的圆心为C，直线
(
为参数)与该圆相交于A，B两点，则
的面积为 .
答案:1/2
13.已知a,b∈R，且a-3b+6=0，则
的最小值为 .
答案:1/4
14.已知a>0，函数
若关于x的方程f(x)=ax恰有2个互异的实数解，则a的取值范围是 .
答案:(4,8)
15.在△ABC中，内角A，B，C所对的边分别为a，b，c.已知 （I）求角B的大小； （II）设a=2，c=3，求b和
.
的值.
答案:本小题主要考查同角三角函数的基本关系，两角差的正弦与余弦公式，二倍角的正弦与余弦公式，以及正弦定理、余弦定理等基础知识，考查运算求解能力．满分13分．看解析》》》
16. (本小题满分13分) 已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16. 现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查. （I）应从甲、乙、丙三个部门的员工中分别抽取多少人？ （II）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查. （i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望； （ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.
答案:本小题主要考查随机抽样、离散型随机变量的分布列与数学期望、互斥事件的概率加法公式等基础知识．考查运用概率知识解决简单实际问题的能力．满分13分．（Ⅰ）解：由已知，甲、乙、丙三个部门的员工人数之比为3∶2∶2，由于采用分层抽样的方法从中抽取7人，因此应从甲、乙、丙三个部门的员工中分别抽取3人，2人，2人．（Ⅱ）（i）解：随机变量X的所有可能取值为0，1，2，3．看解析》》》
17.(本小题满分13分) 如图，AD∕∕BC且AD=2BC， （I）若M为CF的中点，N为EG的中点，求证： （II）求二面角 （III）若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长.
,
且EG=AD，
且CD=2FG，
，DA=DC=DG=2.
；
的正弦值；
答案:（17）本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识．考查用空间向量解决立体几何问题的方法．考查空间想象能力、运算求解能力和推理论证能力．满分13分．依题意，可以建立以D为原点……看解析》》》
18.(本小题满分13分) 设{an}是等比数列，公比大于0，其前n项和为 （I）求 （II）设数列 （i）求 （ii）证明
，
是等差数列. 已知
，
，
，
.
和
的通项公式；
的前n项和为
，
；
.
答案:（18）本小题主要考查等差数列的通项公式，等比数列的通项公式及前n项和公式等基础知识.考查等差数列求和的基本方法和运算求解能力.满分13分.……看解析》》》
19.(本小题满分14分) 设椭圆 （I）求椭圆的方程； （II）设直线l： 若
(a>b>0)的左焦点为F，上顶点为B. 已知椭圆的离心率为
，点A的坐标为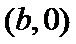
，且
.
与椭圆在第一象限的交点为P，且l与直线AB交于点Q.
(O为原点) ，求k的值.
答案:（19）本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识．考查用代数方法研究圆锥曲线的性质．考查运算求解能力，以及用方程思想解决问题的能力．满分14分．……看解析》》》
20.(本小题满分14分) 已知函数f(x)=ax，g(x)=logax，其中a>1. （I）求函数 （II）若曲线 （III）证明当
的单调区间；
在点
处的切线与曲线
在点
处的切线平行，证明
；
时，存在直线l，使l是曲线
的切线，也是曲线
的切线.
答案:（20）本小题主要考查导数的运算、导数的几何意义、运用导数研究指数函数与对数函数的性质等基础知识和方法.考查函数与方程思想、化归思想.考查抽象概括能力、综合分析问题和解决问题的能力.满分14分.^……看解析》》》
