2018全国二卷理科数学答案解析
1.(1+2i)/(1-2i)=
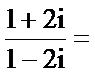
答案:D
2.已知集合 ,则
,则 中元素的个数为
中元素的个数为
答案:A
3.函数
 的图像大致为
的图像大致为

答案:B
4.已知向量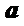 ,
, 满足
满足 ,
, ,则
,则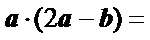
答案:B
5.双曲线 的离心率为
的离心率为 ,则其渐近线方程为
,则其渐近线方程为
答案:A
6.在 中,
中, ,
, ,
, ,则
,则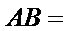
答案:A
7.为计算 ,设计了右侧的程序框图,则在空白框中应填入
,设计了右侧的程序框图,则在空白框中应填入
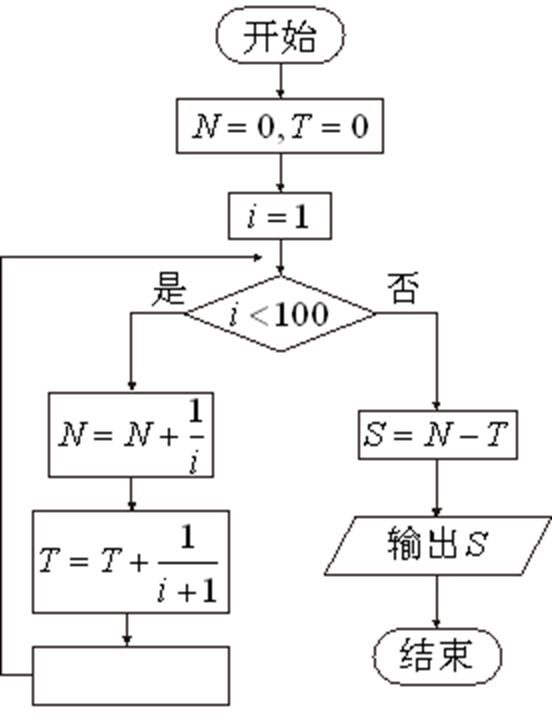
答案:B
8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如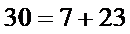 .在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
答案:C
10.若 在
在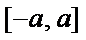 是减函数,则
是减函数,则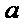 的最大值是
的最大值是
答案:A
12.已知 ,
, 是椭圆
是椭圆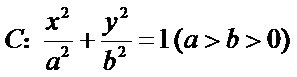 的左、右焦点,
的左、右焦点,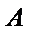 是
是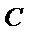 的左顶点,点
的左顶点,点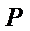 在过
在过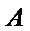 且斜率为
且斜率为 的直线上,
的直线上, 为等腰三角形,
为等腰三角形,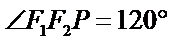 ,则
,则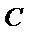 的离心率为
的离心率为
答案:D
y=2x
14.若 满足约束条件
满足约束条件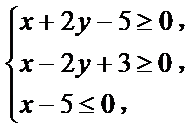 则
则 的最大值为__________.
的最大值为__________.
答案:
9

16.已知圆锥的顶点为 ,母线
,母线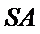 ,
, 所成角的余弦值为
所成角的余弦值为 ,
, 与圆锥底面所成角为45°,若
与圆锥底面所成角为45°,若 的面积为
的面积为 ,则该圆锥的侧面积为__________.
,则该圆锥的侧面积为__________.
答案:
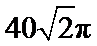
17.(12分)
记
(1)求
(2)求 为等差数列
为等差数列 的前
的前 项和,已知
项和,已知 ,
, .
.
 的通项公式;
的通项公式;
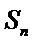 ,并求
,并求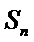 的最小值.
的最小值.
答案:

看解析
19.(12分)设抛物线
(1)求
(2)求过点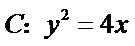 的焦点为
的焦点为 ,过
,过 且斜率为
且斜率为 的直线
的直线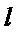 与
与 交于
交于 ,
, 两点,
两点, .
.
 的方程
的方程
 ,
, 且与
且与 的准线相切的圆的方程.
的准线相切的圆的方程.
答案:



20.(12分)
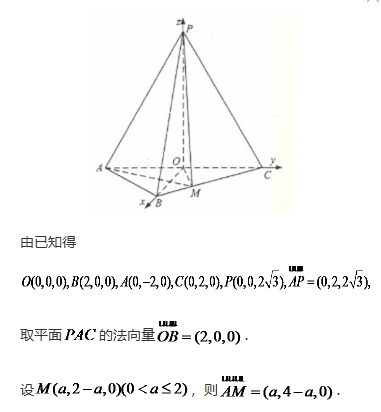
如图,在三棱锥P-ABC中,
(1)证明:
(2)若点
 ,
, ,
, 为
为 的中点.
的中点.
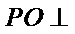 平面
平面 ;
;
 在棱
在棱 上,且二面角
上,且二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.

答案:




21.(12分)
已知函数
(1)若
(2)若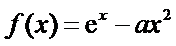 .
.
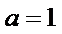 ,证明:当
,证明:当 时,
时, ;
;
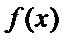 在
在 只有一个零点,求
只有一个零点,求 .
.
答案:






23.[选修4-5:不等式选讲](10分)
设函数
(1)当
(2)若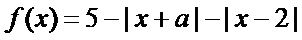 .
.
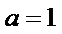 时,求不等式
时,求不等式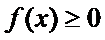 的解集;
的解集;
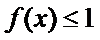 ,求
,求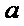 的取值范围.
的取值范围.
答案:
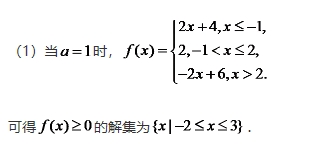




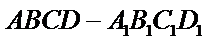 中,
中, ,
,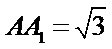 ,则异面直线
,则异面直线 与
与 所成角的余弦值为
所成角的余弦值为 是定义域为
是定义域为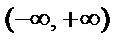 的奇函数,满足
的奇函数,满足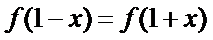 .若
.若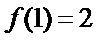 ,则
,则
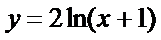 在点
在点 处的切线方程为__________.
处的切线方程为__________. ,
, ,则
,则 __________.
__________. (单位:亿元)的折线图.
(单位:亿元)的折线图.
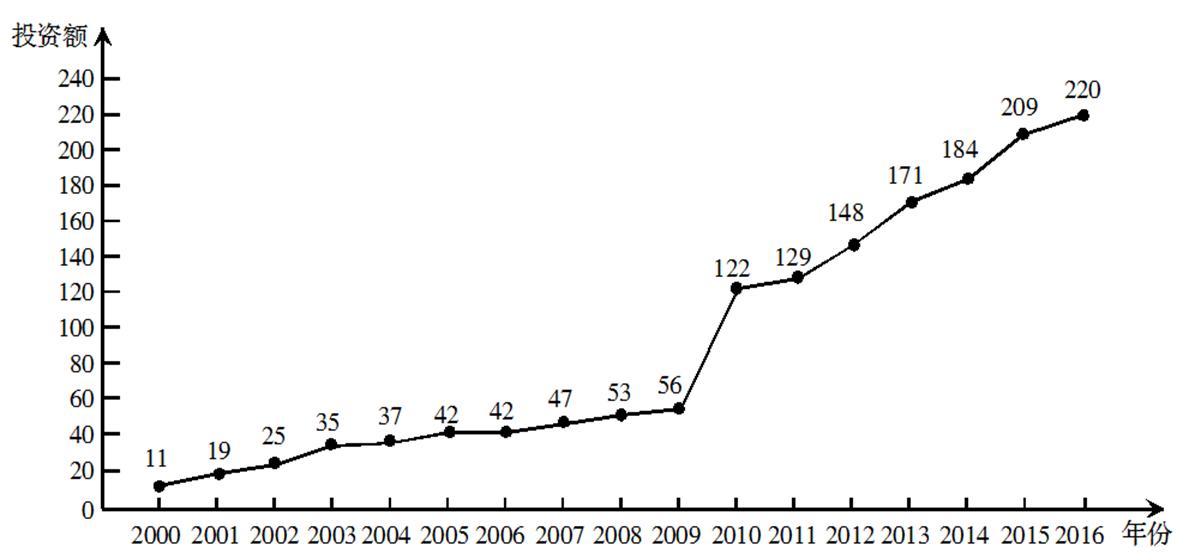
 与时间变量
与时间变量 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量 的值依次为
的值依次为 )建立模型①:
)建立模型①: ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量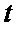 的值依次为
的值依次为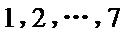 )建立模型②:
)建立模型②: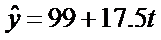 .
.
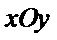 中,曲线
中,曲线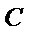 的参数方程为
的参数方程为 (
(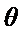 为参数),直线
为参数),直线 的参数方程为
的参数方程为
 (
(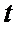 为参数).
为参数).
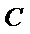 和
和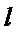 的直角坐标方程;
的直角坐标方程;
 截直线
截直线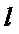 所得线段的中点坐标为
所得线段的中点坐标为 ,求
,求 的斜率.
的斜率.