2020浙江数学高考答案解析
第一题,已知集合P={x|1
答案:B
2.已知a∈R,若a-1+(a-2)i,(i为虚数单位)是实数,则a=_________
答案:C
3.若实数x,y满足约束条件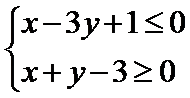 ,则z=x+2y的取值范围是_____
,则z=x+2y的取值范围是_____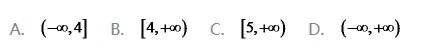
答案:B
4.函数y=xcosx +sinx在区间[-π,+π]的图像大致为_______
答案:A
5. 某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm3 )是
答案:A
6.已知空间中不过同一点的三条直线m,n,l则“m,n,l在同一平面”是m,n两两相交”的
答案:B
7.已知等差数列{an}的前n项的和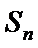 ,公差
,公差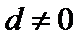 ,
, .记
.记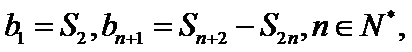 下列等式不可能成立的是
下列等式不可能成立的是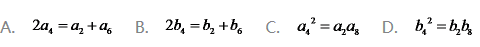
答案:D
8.已知点O(0,0),A(-2,0),B(2,0).设点P满足|PA|-|PB|=2,且P为函数 的图像上的点,则
的图像上的点,则
答案:D
9.已知a,b∈R且ab≠0,若(x-a)(x-b)(x-2a-b)≥0在x≥0上恒成立,则
答案:C
10.设集合S,T, ①对于任意xy∈S,若x≠y,都有xy∈T ②对于任意xy∈T,若x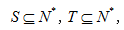 ,S,T中至少有两个元素,且S,T满足:
,S,T中至少有两个元素,且S,T满足:
答案:A
11.已知数列{an}满足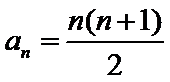 则S3=___________
则S3=___________
答案:
10
80,51
13.已知tanθ=2,则cos2θ=_______,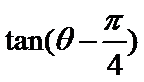 =______.
=______.
答案:
-3/5,1/3
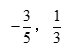
14.已知圆锥展开图的侧面积为2π,且为半圆,则底面半径为______.
答案:
1
15.设直线l:y=kx+b(k>0),圆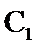 :
: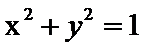 ,
,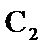 :
: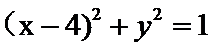 ,若直线l与
,若直线l与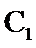 ,
,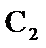 都相切,则k=______;b=______.
都相切,则k=______;b=______.
答案:
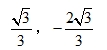
√3/3,-2√3/3
16.一个盒子里有 1个红 1个绿 2个黄四个相同的球,每次拿一个,不放回,拿出红球即停,设拿出黄球的个数为 ,则
,则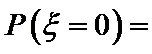 ______;
______;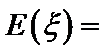 ______;
______;
答案:
1/3,1
17.设e1,e2为单位向量,满足 ,
, ,
,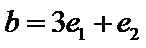 ,设
,设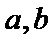 的夹角为
的夹角为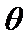 ,则
,则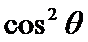 的最小值为_____.
的最小值为_____.
答案:
28/29
18.(本题满分14分) 在锐角△ABC中,角A,B,C的对边分别为a,b,c,且2bsinA =√3a (I)求角B (Ⅱ)求cosA+cosB+cosC的取值范围。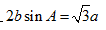
答案:
由正弦定理得:2sinBsin A =√3 sinA

19(本题满分15分) 如图,三棱台DEF-ABC中,面ADFC⊥面ABC,∠ACB=∠ACD=45°,DC=2BC (Ⅰ)证明: (Ⅱ)求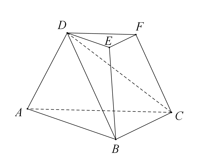
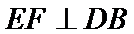 ;
;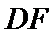 与面
与面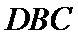 所成角的正弦值。
所成角的正弦值。
答案:
详细解题过程请看解析》》》
20.(本题满分15分) 已知{an},{bn}{cn}中,a1=b1=c1=1, (I)若数列 (Ⅱ)若数列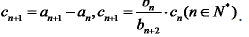
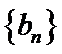 为等比数列,且公比
为等比数列,且公比 ,且
,且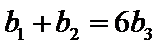 ,求
,求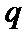 与
与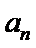 的通项公式;
的通项公式;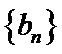 为等差数列,且公差
为等差数列,且公差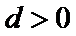 ,证明:
,证明: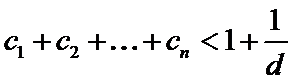
答案:

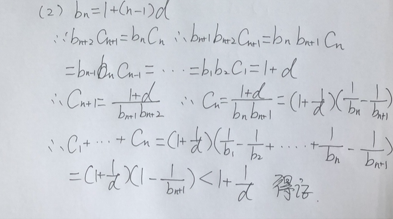



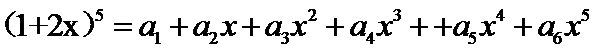 ,则
,则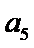 =_______;
=_______;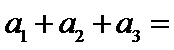 _______.
_______.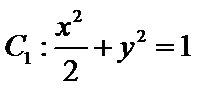 ,抛物线
,抛物线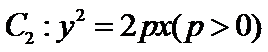 ,点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C于点B,交抛物线C2于M(B,M不同于A).
,点A是椭圆C1与抛物线C2的交点,过点A的直线l交椭圆C于点B,交抛物线C2于M(B,M不同于A).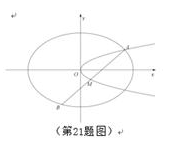
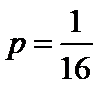 ,求抛物线
,求抛物线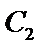 的焦点坐标;
的焦点坐标;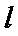 使
使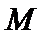 为线段
为线段 的中点;求
的中点;求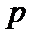 的最大值.
的最大值.

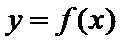 在
在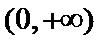 上有唯一零点;
上有唯一零点; 为函数
为函数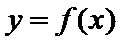 在
在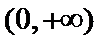 上的零点,证明:
上的零点,证明:
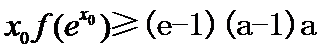 .
.

