2020云南理综考试答案
1.已知集合A={(x,y)|x,y∈N*,y≥x},B={(x,y)|x+y=8},则A∩B中元素个数为
答案:C
2.复数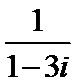 1/1-3i的虚部是
1/1-3i的虚部是
答案:D
3.在一组样本数据中,1,2,3,4出现的频率分别为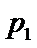 ,
,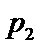 ,
,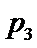 ,
,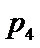 ,且
,且 ,则下面四种情形中,对应样本的标准差最大的一组是
,则下面四种情形中,对应样本的标准差最大的一组是
答案:B
5. 设O为坐标原点,直线 与抛物线
与抛物线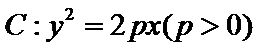 交于D,E两点,若
交于D,E两点,若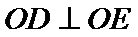 ,则C的焦点坐标为
,则C的焦点坐标为
答案:B
6. 已知向量a,b满足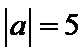 ,
,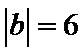 ,
,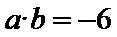 ,则
,则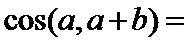
答案:D
7. 在△ABC中,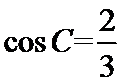 ,
,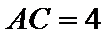 ,
,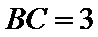 ,则
,则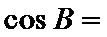
答案:A
8. 右图为某几何体的三视图,则该几何体的表面积是
答案:C
9.已知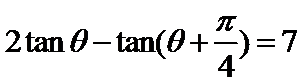 ,则
,则
答案:D
10.若直线 与曲线
与曲线 和圆
和圆 都相切,则
都相切,则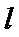 的方程为
的方程为
答案:D
11. 设双曲线
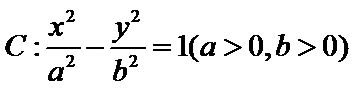 的左、右焦点分别为
的左、右焦点分别为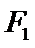 ,
, 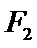 ,离心率为
,离心率为 .
. 
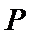 是
是 上一点,且
上一点,且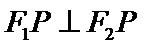 .若△
.若△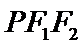 的面积为4,则a=
的面积为4,则a=
答案:A
12.已知55<84,134<85,设a=log53,b=log85,c=1og138,则
答案:A
13. 若x,y满足约束条件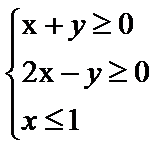 ,则z=3x+2y的最大值为_____.
,则z=3x+2y的最大值为_____.
答案:
7
14. 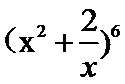 的展开式中常数项是______(用数字作答).
的展开式中常数项是______(用数字作答).
答案:
240
15.已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为____.
答案:
![]()
16.关于函数 ① ② ③ ④ 其中所有真命题的序号是____.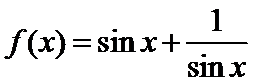 有如下四个命题:
有如下四个命题: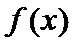 的图像关于
的图像关于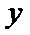 轴对称.
轴对称.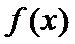 的图像关于原点对称.
的图像关于原点对称.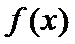 的图像关于直线
的图像关于直线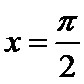 对称.
对称.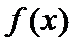 的最小值为2.
的最小值为2.
答案:
②③
17.(12分) 设数列{an}满足a1=3,an-1=3an-4n (1)计算a2,a3,猜想{an}的通项公式并加以证明; (2)求数列{2nan}的前n项和Sn
答案:

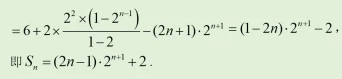

19. (12分) 如图,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且 (1)证明:点 (2)若 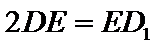 ,
, .
.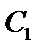 在平面
在平面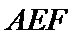 内;
内;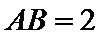 ,
,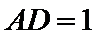 ,
,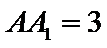 ,求二面角
,求二面角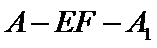 的正弦值.
的正弦值.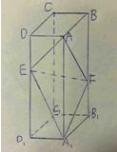
答案:
 更多查看解析》》》
更多查看解析》》》
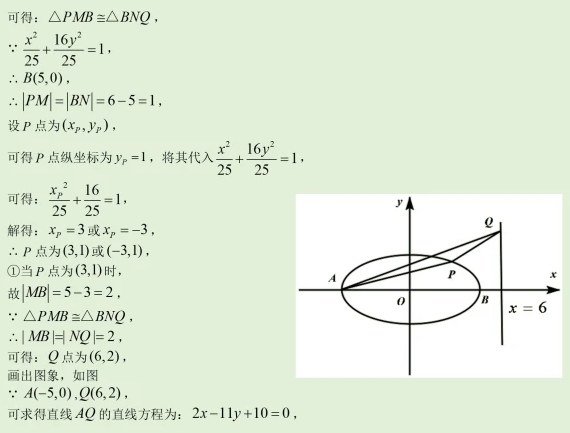
20. (12分) 已知椭圆C: (1)求C的方程; (2)若点P在C上,点Q在直线

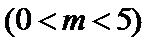 的离心率为
的离心率为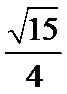 ,A,B分别为C的左、右顶点.
,A,B分别为C的左、右顶点. 上,且
上,且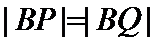 ,
, ,求
,求 的面积.
的面积.
答案:


21. (12分) 设函数f(x)=x3+bx+c,曲线y=f(x)在点 (1)求 (2)若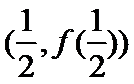 处的切线与
处的切线与 轴重直,
轴重直,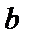 ;
;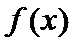 有一个绝对值不大于1的零点,证明:
有一个绝对值不大于1的零点,证明: 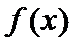 所有零点的绝对值都不大于1.
所有零点的绝对值都不大于1.
答案:



23. [选修4—5:不等式选讲](10分) 设a,b,c∈R,a+b+c=0,abc=1. (1) 证明: (2) 用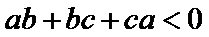 ;
;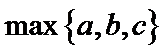 表示
表示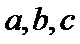 的最大值,证明:
的最大值,证明: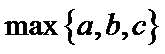
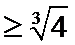
答案:
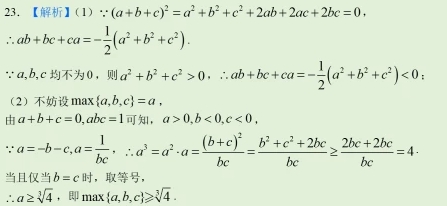



 (
(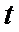 的单位:天)的Logistic模型:
的单位:天)的Logistic模型: ,其中
,其中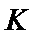 为的最大确诊病例数.当
为的最大确诊病例数.当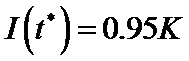 时,标志着已初步遏制疫情,则
时,标志着已初步遏制疫情,则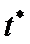 约为(ln19
约为(ln19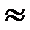 3)
3)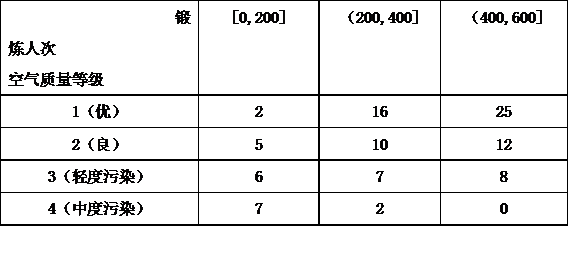
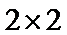 列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?
列联表,并根据列联表,判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关?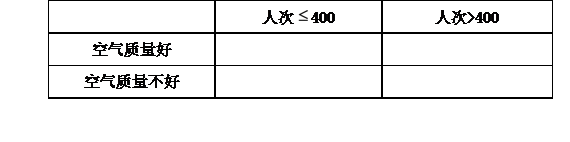
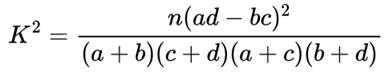 ,
,
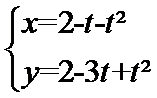 (t为参数且t≠1),C与坐标轴交于A,B两点.
(t为参数且t≠1),C与坐标轴交于A,B两点.