2020高考全国一卷理科数学答案解析
1. 若z=1+i,则|z2-2z|=
答案:D
2.设集合A={x|x2-4<=0},B={x|2x+a<=0}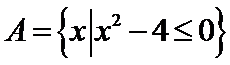 ,
,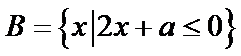 ,且
,且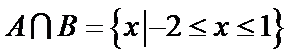 ,则a=
,则a=
答案:B
3. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
答案:C
4.已知A为抛物线C:y2=2px(p>0)上一点,点A到VC的焦点的距离为12,到y轴的距离为9,则p=
答案:C
6.函数f(x)=x4+2x3的图像在点(1,f(1))处的切线方程为
答案:B
7.设函数f(x)=cos(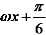 )在[-π,π]的图像大致如下图,则f(x)的最小正周期为
)在[-π,π]的图像大致如下图,则f(x)的最小正周期为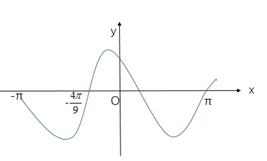
答案:C
8. (x+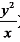 )(x+y)5的展开式中的x3y3系数为
)(x+y)5的展开式中的x3y3系数为
答案:C
9. 已知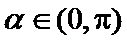 ,且3cos2a-8cosa=5,则sin a=
,且3cos2a-8cosa=5,则sin a=
答案:A
10. 已知A,B,C为球O的球面上的三个点,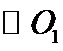 为
为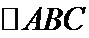 的外接圆,若
的外接圆,若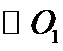 的面积为4π,AB=BC=AC=OO1则球O的表面积为
的面积为4π,AB=BC=AC=OO1则球O的表面积为
答案:A
11. 已知□M:x2+y2-2x-2y-2=0,直线l:2x+y=0,p为l上的动点.过点P作□M的切线PA,PB,切点为A,B,当|PM|□|AB|最小时,直线AB的方程为
答案:D
13.若x,y满足约束条件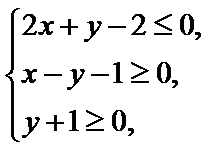 则z=x+7y的最大值为________。
则z=x+7y的最大值为________。
答案:
1
14.设a,b为单位向量,且 ︱a+b︱=1,则︱a-b︱=________。
︱a+b︱=1,则︱a-b︱=________。
答案:
√3
15.已知F为双曲线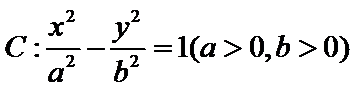 的右焦点,A为C的右顶点,B为C上的点,且BF垂直于x轴,若AB的斜率为3,则C的离心率为__________.
的右焦点,A为C的右顶点,B为C上的点,且BF垂直于x轴,若AB的斜率为3,则C的离心率为__________.
答案:
2
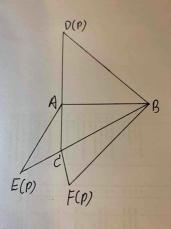
16.如图,在三棱锥P-ABC的平面展开图中, ,
,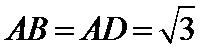 ,
,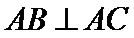 ,
,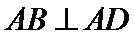 ,
,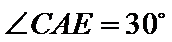 ,则
,则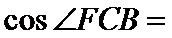 ________.
________.
答案:
- 1/4
17.(12分) 设{an}是公比不为1的等比数列,a1为a2,a3的等差中项. (1) 求{an}的公比; (2) 若a1=1,求数列{nan}的前n项和.
答案:
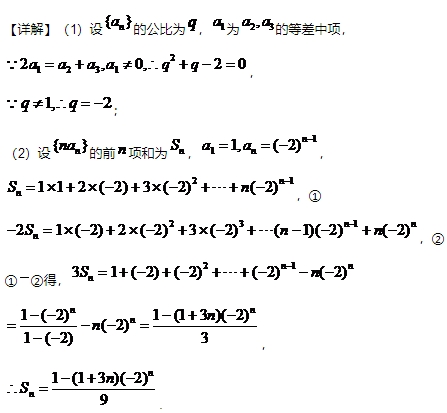
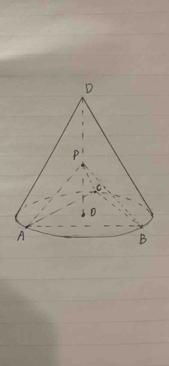
18.(12分)如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD, (1)证明:PA⊥平面PBC; (2)求二面角B-PC-E的余弦值.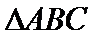 是底面的内接正三角形,P为DO上一点,
是底面的内接正三角形,P为DO上一点,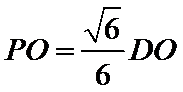 .
.
答案:

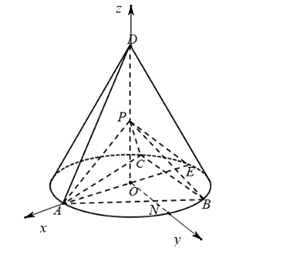
 OA为x轴,ON为y轴建立如图所示的空间直角坐标系,
OA为x轴,ON为y轴建立如图所示的空间直角坐标系,
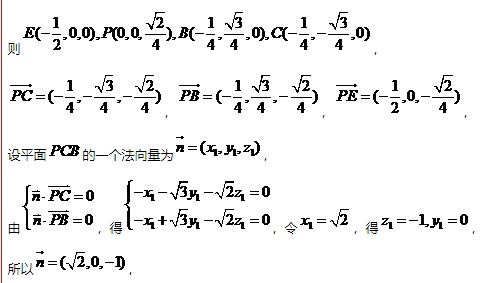

(1)根据独立事件的概率乘法公式可求得事件“甲连胜四场”的概率;
(2)计算出四局以内结束比赛的概率,然后利用对立事件的概率公式可求得所求事件的概率;
(3)列举出甲赢的基本事件,结合独立事件的概率乘法公式计算出甲赢的概率,由对称性可知乙赢的概率和甲赢的概率相等,再利用对立事件的概率可求得丙赢的概率.


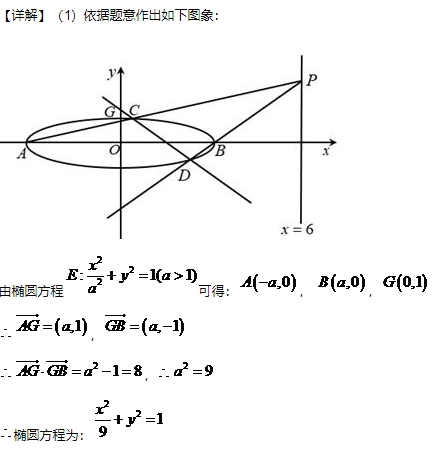
20.(12分) 已知A,B分别为椭圆 (1)求E的方程 (2)证明:直线CD过定点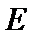 :
: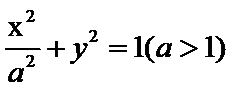 的左、右顶点,G为E上顶点,
的左、右顶点,G为E上顶点,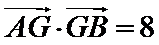 .P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
.P为直线x=6上的动点,PA与E的另一交点为C,PB与E的另一交点为D.
答案:

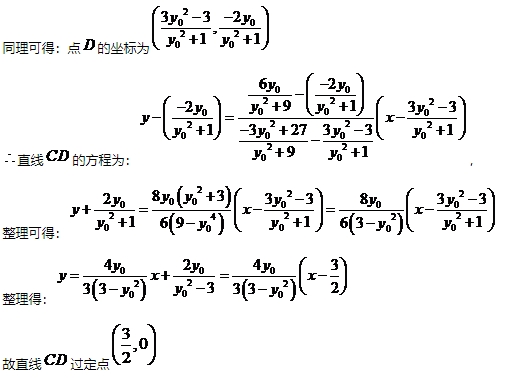
21.(12分) 已知函数f(x)=ex+ax2-x. (1) 当 (2) 当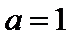 时,讨论
时,讨论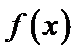 的单调性;
的单调性;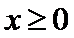 时,
时,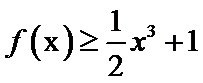 ,求a的取值范围.
,求a的取值范围.
答案:
(1)由题意首先对函数二次求导,然后确定导函数的符号,最后确定原函数的单调性即可.
(2)首先讨论x=0情况,然后分离参数,构造新函数,结合导函数研究构造所得的函数的最大值即可确定实数a的取值范围.



第1小题正确答案

第2小题正确答案

本题考查参数方程与普通方程互化,极坐标方程与直角坐标方程互化,合理消元是解题的关系,要注意曲线坐标的范围,考查计算求解能力,属于中档题.
23. [选修4—5:不等式选讲](10分) 已知函数f(x)=|3x+1|-2|x-1|. (1) 画出y=f(x)的图像; (2) 求不等式f(x)>f(x+1)的解集.
答案:
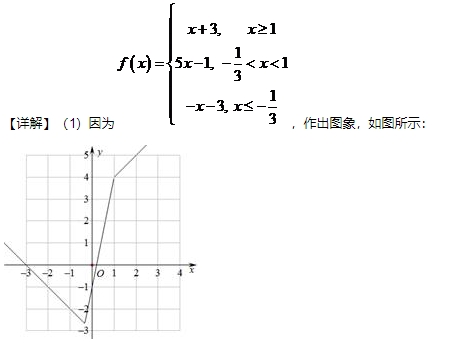
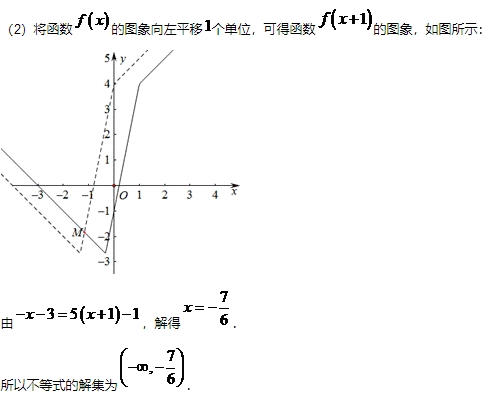 本题主要考查画分段函数的图象,以及利用图象解不等式,意在考查学生的数形结合能力,属于基础题.
本题主要考查画分段函数的图象,以及利用图象解不等式,意在考查学生的数形结合能力,属于基础题.



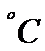 )的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据
)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据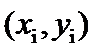
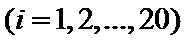 得到下面的散点图:
得到下面的散点图:
 .
.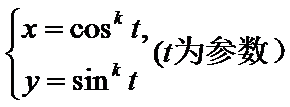 ,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为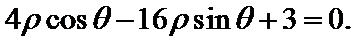
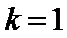 时,
时,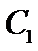 是什么曲线?
是什么曲线?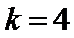 时,求
时,求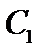 与
与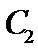 的公共点的直角坐标.
的公共点的直角坐标.