2019全国二卷数学理科答案
1.设集合A={x|x2–5x+6>0},B={x|x–1<0},则A∩B=
答案:A
5.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是
答案:A
6.若a>b,则
答案:C
8.若抛物线y2=2px(p>0)的焦点是椭圆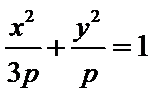 的一个焦点,则p=
的一个焦点,则p=
答案:D
9.下列函数中,以 为周期且在区间(
为周期且在区间( ,
, )单调递增的是
)单调递增的是
答案:A
10.已知α∈(0,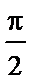 ),2sin2α=cos2α+1,则sinα=
),2sin2α=cos2α+1,则sinα=
答案:B
11.设F为双曲线C: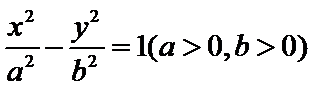 的右焦点,
的右焦点,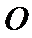 为坐标原点,以
为坐标原点,以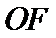 为直径的圆与圆
为直径的圆与圆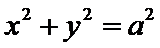 交于P,Q两点.若
交于P,Q两点.若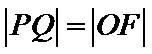 ,则C的离心率为
,则C的离心率为
答案:A
12.设函数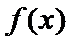 的定义域为R,满足
的定义域为R,满足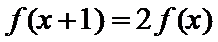 ,且当
,且当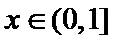 时,
时,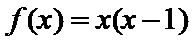 .若对任意
.若对任意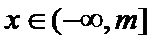 ,都有
,都有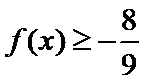 ,则m的取值范围是
,则m的取值范围是
答案:B
14.已知 是奇函数,且当
是奇函数,且当 时,
时, .若
.若 ,则
,则 __________.
__________.
答案:-3
15.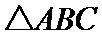 的内角
的内角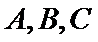 的对边分别为
的对边分别为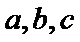 .若
.若 ,则
,则 的面积为_________.
的面积为_________.
答案:
6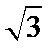
17.(12分) 如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1. (1)证明:BE⊥平面EB1C1; (2)若AE=A1E,求二面角B–EC–C1的正弦值.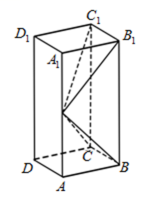
19.(12分) 已知数列{an}和{bn}满足a1=1,b1=0, (1)证明:{an+bn}是等比数列,{an–bn}是等差数列; (2)求{an}和{bn}的通项公式.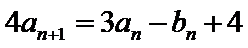 ,
,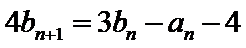 .
.
20.(12分) 已知函数 (1)讨论f(x)的单调性,并证明f(x)有且仅有两个零点; (2)设x0是f(x)的一个零点,证明曲线y=lnx在点A(x0,lnx0)处的切线也是曲线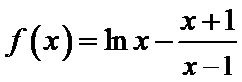 .
.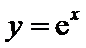 的切线.
的切线.
23.[选修4—5:不等式选讲](10分) 已知 (1)当 (2)若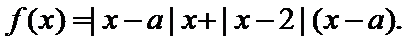
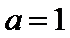 时,求不等式
时,求不等式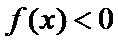 的解集;
的解集;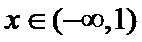 时,
时,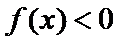 ,求
,求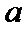 的取值范围.
的取值范围.



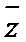 对应的点位于
对应的点位于 =(2,3),
=(2,3), =(3,t),
=(3,t), =1,则
=1,则 =
=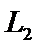 点的轨道运行.
点的轨道运行.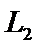 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,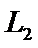 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程: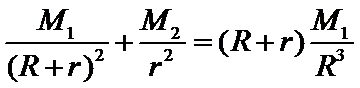 .设
.设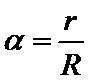 ,由于
,由于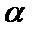 的值很小,因此在近似计算中
的值很小,因此在近似计算中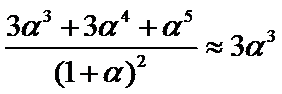 ,则r的近似值为
,则r的近似值为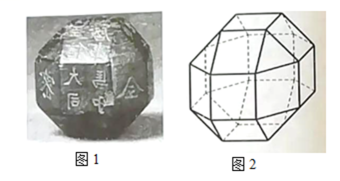
 .记M的轨迹为曲线C.
.记M的轨迹为曲线C.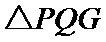 是直角三角形;
是直角三角形;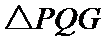 面积的最大值.
面积的最大值.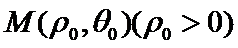 在曲线
在曲线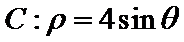 上,直线l过点
上,直线l过点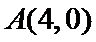 且与
且与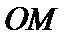 垂直,垂足为P.
垂直,垂足为P.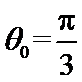 时,求
时,求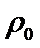 及l的极坐标方程;
及l的极坐标方程;