24.小云在学习过程中遇到一个函数y=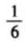 |x(x2-x+1)(x≥-2).
|x(x2-x+1)(x≥-2).
下面是小云对其探究的过程,请补充完整:
(1)当-2≤x<0时,
对于函数y1=|x|,即y1=-x,当-2≤x<0时,y随x的增大而________且y1>0;
对于函数y2=x2-x+1,当-2≤x<0时,y2随x的增大而_________且y2>0;
结合上述分析,进步探究发现,对于函数y,当-2≤x<0时,y随x的增大而_______
(2)当x≥0时,
对于函数y,当x≥0时,y与x的几组对应值如下表:
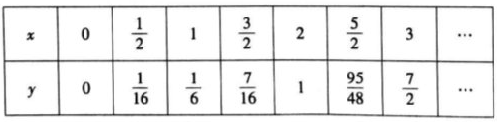
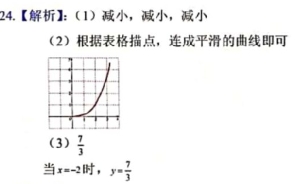
结合上表,进一步探究发现,当x≥0时,y随x的增大而增大,在平面直角坐标系xOy中,画出当x≥0时的函数y的图象
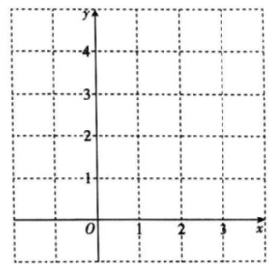
(3)过点(0,m)(m>0)作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数y=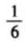 |x|(x2-x+1)(x≥-2)的图象有两个交点,则m的最大值是______________。
|x|(x2-x+1)(x≥-2)的图象有两个交点,则m的最大值是______________。


- 1
5.正五边形的外角和为
- 2
23.如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.

(1)求证:∠ADC=∠AOF;
(2)若sinC=3,BD=8,求EF的长
- 3
10.已知关于x的方程x2+2x+k=0有两个相等的实数根,则k的值是__________
- 4
12.方程组
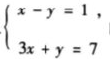 的解为________
的解为________ - 5
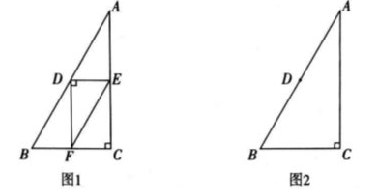
27.在△ABC中,∠C=90°,AC>BC,D是AB的中点E为直线AC上一动点,连接DE,过点D作DF⊥DE,交直线BC于点F,连接EF
(1)如图1,当E是线段AC的中点时,设AE=a,BF=b,求EF的长(用含a,b的式子表示);
(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.
- 6
13.在平面直角坐标系xOy中,直线y=x与双曲线y=
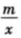 交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为__________
交于A,B两点.若点A,B的纵坐标分别为y1,y2,则y1+y2的值为__________ - 7
19.已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
- 8
4.下列图形中,既是中心对称图形也是轴对称图形的是
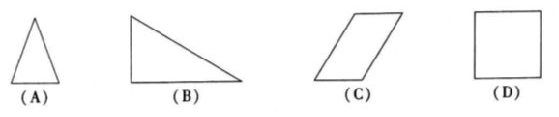
- 9
24.小云在学习过程中遇到一个函数y=
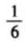 |x(x2-x+1)(x≥-2).
|x(x2-x+1)(x≥-2). 下面是小云对其探究的过程,请补充完整:
(1)当-2≤x<0时,
对于函数y1=|x|,即y1=-x,当-2≤x<0时,y随x的增大而________且y1>0;
对于函数y2=x2-x+1,当-2≤x<0时,y2随x的增大而_________且y2>0;
结合上述分析,进步探究发现,对于函数y,当-2≤x<0时,y随x的增大而_______
(2)当x≥0时,
对于函数y,当x≥0时,y与x的几组对应值如下表:

结合上表,进一步探究发现,当x≥0时,y随x的增大而增大,在平面直角坐标系xOy中,画出当x≥0时的函数y的图象

(3)过点(0,m)(m>0)作平行于x轴的直线l,结合(1)(2)的分析,解决问题:若直线l与函数y=
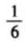 |x|(x2-x+1)(x≥-2)的图象有两个交点,则m的最大值是______________。
|x|(x2-x+1)(x≥-2)的图象有两个交点,则m的最大值是______________。 - 10
25.小云统计了自己所住小区5月1日至30日的厨余垃圾分出量(单位:千克),相关信息如下:
a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:

b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:

(1)该小区5月1日至30日的厨余垃圾分出量的平均数约为___________(结果取整数);
(2)已知该小区4月的厨余垃圾分出量的平均数为60,则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的________倍(结果保留小数点后一位);
(3)记该小区5月1日至10日的厨余垃圾分出量的方差为
 ,5月11日至20日的厨余垃圾分出量的方差为
,5月11日至20日的厨余垃圾分出量的方差为 ,5月21日至30日的厨余垃圾分出量的方差为
,5月21日至30日的厨余垃圾分出量的方差为 .直接写出
.直接写出 ,
, ,
, 的大小关系
的大小关系
