19. (12分)
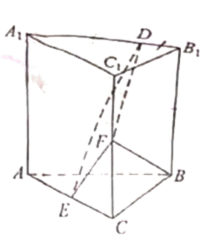
已知直三棱柱ABC-A1B1C1.中,侧面AA1B1B为正方形, AB= BC = 2, E, F分别为AC和CC1的中点,D为棱A1B1上的点,BF丄A1B1.
(1) 证明:BF⊥DE;
⑵ 当为B1D何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?
正确答案
(1)直棱柱ABC-A1B1C1,侧面AA1B1B为正方形所以A1B1=B1B=AB=BC=2所以侧面BB1C1C为正方形取BC中点M,连接B1M和EM因为F为CC1重点,所以B1M⊥BF由已知BF⊥A1B1……更多请查看解析》》》
(1)直棱柱ABC-A1B1C1,侧面AA1B1B为正方形所以A1B1=B1B=AB=BC=2所以侧面BB1C1C为正方形取BC中点M,连接B1M和EM因为F为CC1重点,所以B1M⊥BF由已知BF⊥A1B1……更多请查看解析》》》
查看解析
继续答题:下一题


