2020年天津高考数学试卷及其解析
1.设全集U={-3,-2,-1,0,1,2,3},集合A={-1,0,1,2},B={-3,0,2,3},则A∩(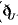 B)=
B)=
答案:C
3.函数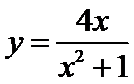 的图象大致为
的图象大致为
答案:A
4.从一批零件中抽取80个,测量其直径(单位: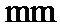 ),将所得数据分为9组:
),将所得数据分为9组: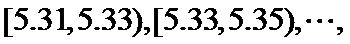
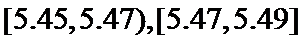 ,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间
,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间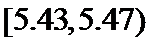 内的个数为
内的个数为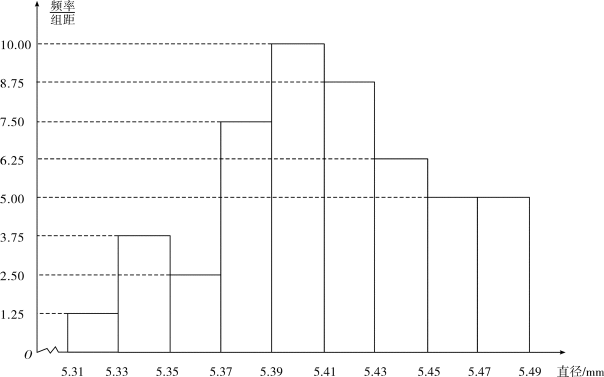
答案:B
5.若棱长为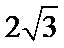 的正方体的顶点都在同一球面上,则该球的表面积为
的正方体的顶点都在同一球面上,则该球的表面积为
答案:C
6.设a=30.7,b=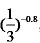 ,c=㏒0.70.8.,则abc的大小关系为
,c=㏒0.70.8.,则abc的大小关系为
答案:D
7.设双曲线C的方程为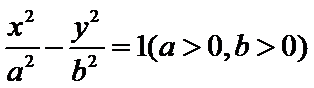 ,过抛物线y2=4x的焦点和点
,过抛物线y2=4x的焦点和点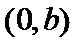 的直线为
的直线为 .若
.若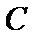 的一条渐近线与
的一条渐近线与 平行,另一条渐近线与
平行,另一条渐近线与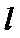 垂直,则双曲线
垂直,则双曲线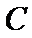 的方程为
的方程为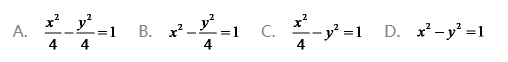
答案:D
8.已知函数 ① ② ③把函数 其中所有正确结论的序号是 .给出下列结论:
.给出下列结论: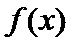 的最小正周期为
的最小正周期为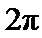 ;
;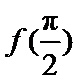 是
是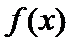 的最大值;
的最大值;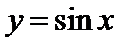 的图象上所有点向左平移
的图象上所有点向左平移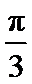 个单位长度,可得到函数
个单位长度,可得到函数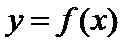 的图象.
的图象.
答案:B
9.已知函数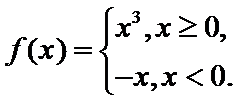 若函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,则k的取值范围是
若函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,则k的取值范围是
答案:D
3-2i
10
12.已知直线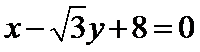 和圆x2+y2=r2(r>0)相交于A,B两点.若|AB|=6,则r的值为_________.
和圆x2+y2=r2(r>0)相交于A,B两点.若|AB|=6,则r的值为_________.
答案:
5
13.已知甲、乙两球落入盒子的概率分别为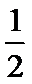 和
和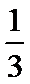 .假定两球是否落入盒子互不影响,则甲、乙两球都落入盒子的概率为_________;甲、乙两球至少有一个落入盒子的概率为_________.
.假定两球是否落入盒子互不影响,则甲、乙两球都落入盒子的概率为_________;甲、乙两球至少有一个落入盒子的概率为_________.
答案:
1/6;2/3
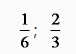
14.已知a>0,b>0,且ab=1,则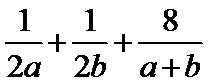 的最小值为_________.
的最小值为_________.
答案:
4
15.如图,在四边形ABCD中,∠B=60°,AB=3,BC=6,且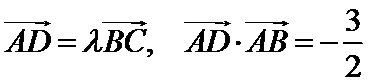 ,则实数
,则实数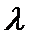 的值为_________,若
的值为_________,若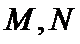 是线段
是线段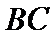 上的动点,且
上的动点,且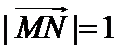 ,则
,则 的最小值为_________.
的最小值为_________.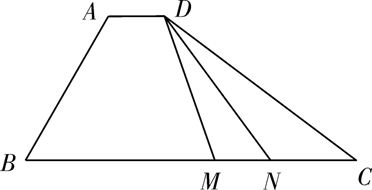
答案:
1/6;13/2
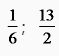
16.(本小题满分14分) 在△ABC中,角A,B,C所对的边分别为a,b,c.已知 (Ⅰ)求角 (Ⅱ)求 (Ⅲ)求 .
. 的大小;
的大小;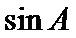 的值;
的值;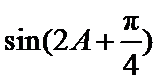 的值.
的值.
答案:
(Ⅰ)在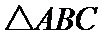 中,由余弦定理及
中,由余弦定理及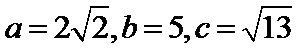 ,有
,有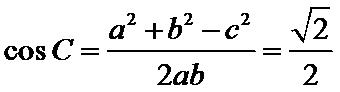 .又因为
.又因为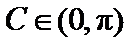 ,所以
,所以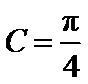 .
.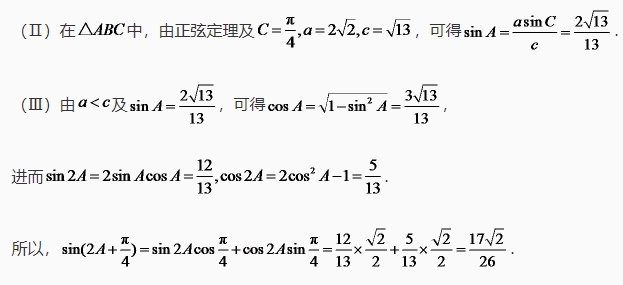
依题意,以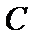 为原点,分别以
为原点,分别以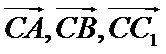 的方向为
的方向为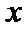 轴,
轴,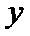 轴,
轴,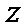 轴的正方向建立空间直角坐标系(如图),可得
轴的正方向建立空间直角坐标系(如图),可得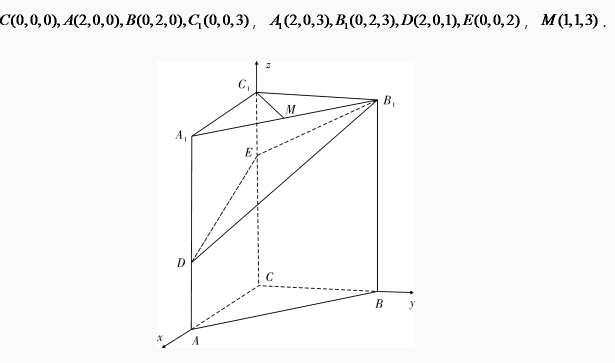


18.(本小题满分15分) 已知椭圆 (Ⅰ)求椭圆的方程; (Ⅱ)已知点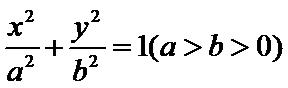 的一个顶点为
的一个顶点为 ,右焦点为
,右焦点为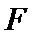 ,且
,且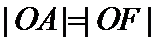 ,其中
,其中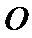 为原点.
为原点.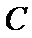 满足
满足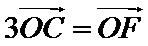 ,点
,点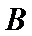 在椭圆上(
在椭圆上(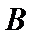 异于椭圆的顶点),直线
异于椭圆的顶点),直线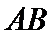 与以
与以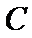 为圆心的圆相切于点
为圆心的圆相切于点 ,且
,且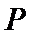 为线段
为线段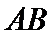 的中点.求直线
的中点.求直线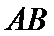 的方程.
的方程.
答案:(Ⅰ)由已知可得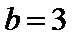 .记半焦距为
.记半焦距为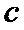 ,由
,由 可得
可得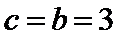 .又由
.又由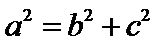 ,可得
,可得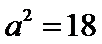 .所以,椭圆的方程为
.所以,椭圆的方程为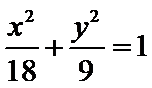 .更多请查看解析
.更多请查看解析
(Ⅰ)设等差数列 的公差为
的公差为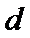 ,等比数列
,等比数列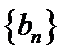 的公比为
的公比为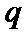 .由
.由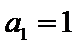 ,
,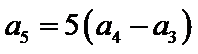 ,可得
,可得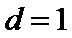 ,从而
,从而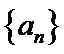 的通项公式为
的通项公式为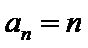 .由
.由 ,又
,又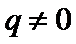 ,更多查看解析》》》
,更多查看解析》》》
(Ⅰ)(i)当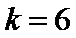 时,
时,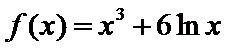 ,故
,故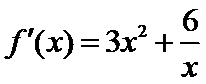 .可得
.可得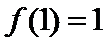 ,
, ,所以曲线
,所以曲线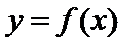 在点
在点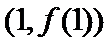 处的切线方程为
处的切线方程为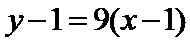 ,即
,即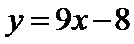 .更多请查看解析
.更多请查看解析



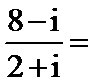 _________.
_________.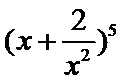 的展开式中,x2的系数是_________.
的展开式中,x2的系数是_________.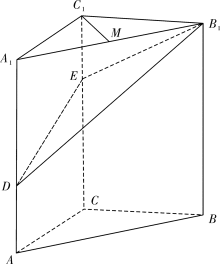
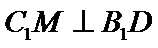 ;
;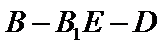 的正弦值;
的正弦值;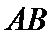 与平面
与平面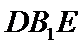 所成角的正弦值.
所成角的正弦值.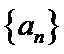 的前
的前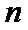 项和为
项和为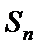 ,求证:
,求证: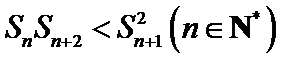 ;
;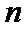 ,设
,设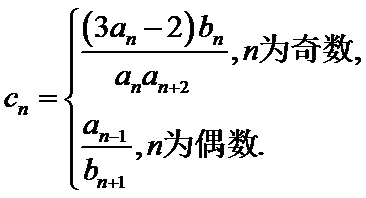 求数列
求数列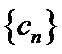 的前
的前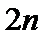 项和.
项和.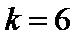 时,
时,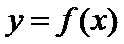 在点
在点 处的切线方程;
处的切线方程;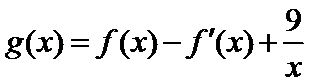 的单调区间和极值;
的单调区间和极值;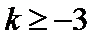 时,求证:对任意的
时,求证:对任意的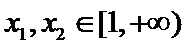 ,且
,且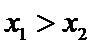 ,有
,有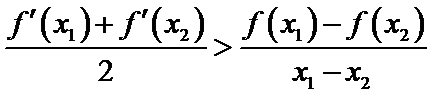 .
.